জ্যামিতির ইতিহাসের গালিচা

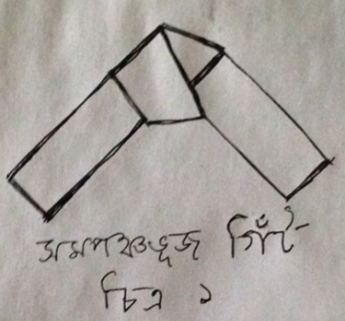
আমরা সবাই জানি যে মানুষের উৎস আফ্রিকায়। তবে আফ্রিকা যে মানুষের গণিত ভাবনারও অন্যতম উৎস, সে কথাটা সবাই হয়তো জানেন না। কঙ্গোর নিবাসী ঐতিহাসিক এবং মিশর বিশেষজ্ঞ থিওফিলিক ওবেঙ্গা লক্ষ্য করেছেন যে প্রাচীন মিশরের জ্যামিতিচর্চার ঐতিহ্যের সঙ্গে সাহারার দক্ষিণে আফ্রিকার আদিম মানুষের জ্যামিতির ঐতিহ্য অঙ্গাঙ্গীভাবে জড়িত। আফ্রিকার বালি শিল্প আর বোনার কাজে দেখা যায় ম্যাজিক স্কোয়ার আর বহুভুজ দিয়ে তৈরি নকশার জালের বহু উদাহরণ। টেলেমের তাঁতিরা তাদের গিঁট তৈরিতে সমপঞ্চভূজ ব্যবহার করেন (চিত্র-১)। এই প্রবন্ধে আমরা শুধু সাহারার দক্ষিণ অঞ্চলের বুনন শিল্পের নিদর্শনের মধ্যে দিয়ে পাইথাগোরাসের উপপাদ্যের মূল খোঁজার চেষ্টা করব।

     গণিতের ইতিহাসে দেখা যায় চিন্তাভাবনা বয়ে চলেছে বিমূর্ত থেকে মূর্তের দিকে আবার কখনও বা বিপরীত পথে। যেমন বক্র জ্যামিতিতে মহামান্য গণিতজ্ঞ কার্ল ফ্রিডরিশ গাউসের আগ্রহ জন্মেছিল হ্যানোভারে জমি নিরীক্ষণের কাজের সূত্রে। পাইথাগোরাসের উপপাদ্যের ইতিহাস বিমূর্ত আর মূর্ত ভাবনার যোগাযোগের একটি চমৎকার উদাহরণ। সামোসের অধিবাসী পাইথাগোরাস (খ্রীষ্টপূর্ব ষষ্ঠ শতাব্দী) এর নামে এই উপপাদ্য। প্রখ্যাত ঐতিহাসিক এবং নৃতাত্ত্বিক গবেষক শেখ আন্টা ডি-ওপ এর মতে মিশরে ভ্রমণ করার সময় পাইথাগোরাস এই উপপাদ্যের মূল প্রতিপাদ্যের নানা ব্যবহারিক উদাহরণ লক্ষ্য করেছিলেন। আমরা এই উপপাদ্যের ব্যবহার দেখতে পাই সাহারার দক্ষিণে নানা কারুশিল্পে।

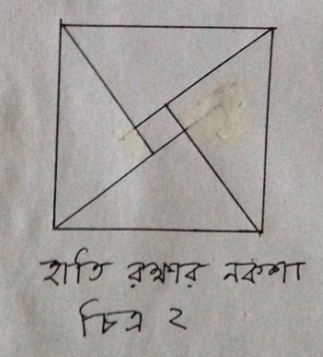
কঙ্গোতে হাতি রক্ষার নকশা  

প্রাচীন কুবা রাজত্বের বুশাঙ্গো মানুষেরা চিত্র-২ তে দেখানো নকশার নাম দেয় হাতি রক্ষার নকশা। এই নকশাটিকে পাইথাগোরাসের উপপাদ্য প্রমাণ করার ক্ষেত্রে এক গুরুত্বপূর্ণ সংযোজন বলে ধরা যেতে পারে।

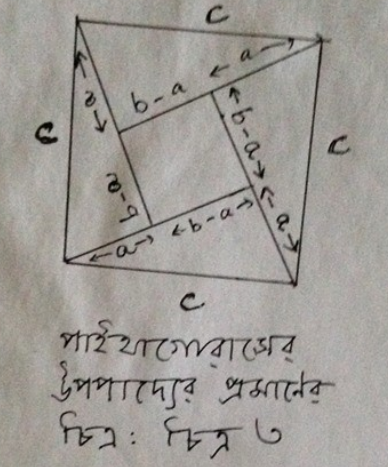
প্রাচীন ভারতের বিখ্যাত গণিতজ্ঞ ভাস্কর (দ্বাদশ শতাব্দী) এই একই চিত্র ব্যবহার করে পাইথাগোরাসের উপপাদ্য প্রমাণ করেন। প্রমাণটা এইভাবে করা যায়, (চিত্র-৩ দ্রষ্টব্য)।

(a – b)² + 4 * ½ * ab = c²

a² + b² – 2ab + 2ab = c²

a² + b² = c²

আমরা এবারে পিথাগোরাসের উপপাদ্যের আর একটা ব্যবহারিক উদাহরণ দেখি।

জানজিবারের মাদুর

জানজিবার দেশে প্রাচীন কাল থেকে ব্যবহৃত মাদুরের মধ্যে একটা বিশেষ নকশায় চোখ বুলিয়ে নেয়া যাক একবার (চিত্র–৪)।

     ভেতর আর বাইরের দুটো সমচতুর্ভূজ আমরা আবার আঁকলাম (চিত্র–৫)। এবারে আমরা পেলাম ABCD সমচতুর্ভূজের মধ্যে আঁকা WXYZ সমচতুর্ভূজ। বড় সমচতুর্ভূজের ক্ষেত্রের আয়তন হল ছোট সমচতুর্ভূজ আর চারটে সমকোণী ত্রিভুজের ক্ষেত্রের আয়তনের সমান। তাহলে পাওয়া গেল–

(a + b)² =  4(1/2 * ab) + c² = 2ab + c²

আবার সেই একই ক্ষেত্রের আয়তন হবে,

(a + b)² = a² + b² + 4(1/2 * ab) (চিত্র – ৬)

                                                             = a² + b² +  2ab

এই দুই সমীকরণ থেকে পাই,

a² + b² = c²

 চিত্র ৬

     এটা ঠিক জানা নেই যে আফ্রিকার হস্তশিল্পের ঐতিহ্য জ্যামিতিক সূত্রের গঠনে ঠিক কতটা প্রভাব বিস্তার করেছে। তবে একই চিন্তার প্রয়োগ মানুষের বিচিত্র কর্মকাণ্ডে প্রভাব ফেলেছে দেখে আশ্চর্য লাগে। একে শিক্ষার কাজেও ব্যবহার করা যেতে পারে যার মানে হল বয়নশিল্পের নানা নকশা বা প্যাটার্ন দেখিয়ে ছাত্রছাত্রীদেরও দুরূহ জ্যামিতিক সূত্রকেও প্রাঞ্জলভাবে বোঝানো যায়। উৎসাহীরা এই ব্যাপারে আরও জানার নিম্নলিখিত বইটা পড়ে দেখতে পারেন।

Geometry from Africa, Mathematical and Educational Explorations: Paulus Gerdes, The Mathematical Association of America, 1999

সম্পাদকঃ লেখাটি টাইপ করে আমাদের সাহায্য করেছেন অমৃতা গঙ্গোপাধ্যায়।